- Услуги
- Цена и срок
- О компании
- Контакты
- Способы оплаты
- Гарантии
- Отзывы
- Вакансии
- Блог
- Справочник
- Заказать консультацию
Заказать консультацию
Свойства нормального распределения
Говорят, что случайная величина ξ распределена нормально (normal distribution), если ее плотность распределения вероятностей имеет вид:

График плотности нормального распределения приведен на рис. 1.
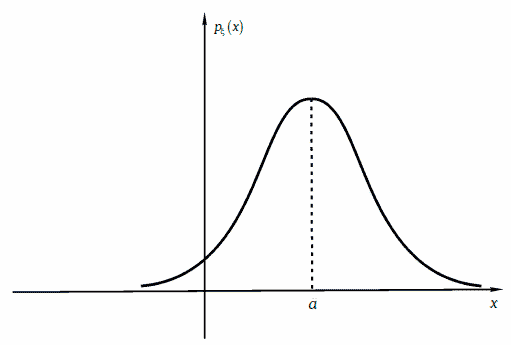
Рис. 1. График плотности нормального распределения
Основные свойства нормального распределения
1. Если случайная величина ξ распределена нормально с плотностью
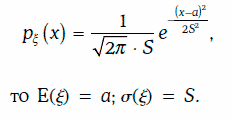 2. Плотность нормально распределенной случайной величины симметрична относительно математического ожидания этой случайной величины, т. е. асимметрия a(ξ) = 0.
2. Плотность нормально распределенной случайной величины симметрична относительно математического ожидания этой случайной величины, т. е. асимметрия a(ξ) = 0.
В частности,
![]()
Эксцесс нормального распределения всегда равен 3.
3. Вероятность того, что нормально распределенная случайная величина будет отличаться от своего ожидаемого значения на величину, не превышающую одного, двух или трех ее стандартных отклонений, равна 68,3, 95,5 и 99,75 % соответственно.
4. Если случайная величина ξ распределена нормально с параметрами (a, S), то случайная величина
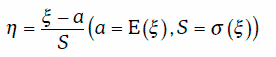 распределена нормально с параметрами (0, 1), т. е. имеет стандартное нормальное распределение.
распределена нормально с параметрами (0, 1), т. е. имеет стандартное нормальное распределение.



Статьи по теме
- Краткий обзор Нового базельского соглашения по капиталу
- Модель управления активами и пассивами (ALM)
- Метод сигналов
- Подход на основе регрессионного анализа
- Модели возникновения финансовых кризисов
- Минимальные требования к достаточности капитала с учетом кредитного и рыночного рисков
- Подход на основе внутренних моделей банков. Верификация моделей расчета VaR по историческим данным
- Подход на основе внутренних моделей банков. Количественные критерии
- Подход на основе внутренних моделей банков. Качественные критерии
Полезные статьи









Узнайте цену услуг:
Узнай цену консультации
"Да забей ты на эти
дипломы и экзамены!”
(дворник Кузьмич)

