Модели Рендлмана-Барттера, Васичека и Кокса- Ингерсолла-Росса

Модель Рендлмана-Барттера (Rendleman-Bartter model)

Предполагается, что краткосрочная процентная ставка rτ в мире, нейтральном к риску, определяется геометрическим броуновским движением

и удовлетворяет начальному условию rt = r0.

В этом случае краткосрочная процентная ставка rт распределена логнормально с параметрами:

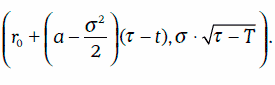Для оценки стоимости финансовых инструментов, производных от процентной ставки, можно использовать стандартную биномиальную модель с показателями

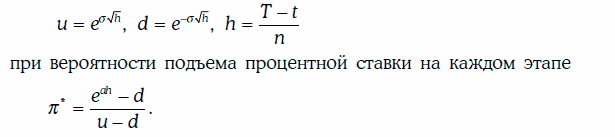
Замечание. В модели Рендлмана-Барттера ожидаемое значение краткосрочной процентной ставки rτ равно 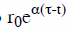. Это означает, что в модели не учитывается эффект возвращения к среднему (mean reversion): если процентная ставка сильно отклоняется от некоторого долгосрочного среднего значения, то в дальнейшем проявляется тенденция возвращения процентной ставки к среднему значению.

Модель Васичека (Vasicek model)

Предполагается, что краткосрочная процентная ставка в мире, нейтральном к риску, определяется стохастическим дифференциальным уравнением

и удовлетворяет начальному условию rt = r0.

Это означает, что краткосрочная процентная ставка rτ распределена нормально с параметрами:

Стоимость облигации с нулевым купоном номиналом 1 долл. и датой погашения Т может быть найдена по формуле, так как в данном случае:

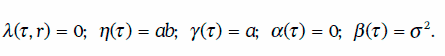
В условиях модели Васичека стоимость европейских опционов колл (сτ) и пут (рτ) в момент τ на облигацию с нулевым купоном можно найти по формулам:

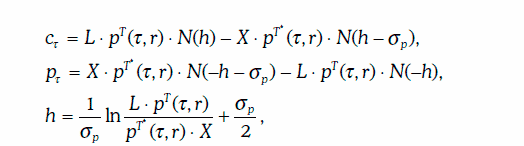
Замечание. Для доказательства достаточно проверить, что cτ и pτ удовлетворяют дифференциальному уравнению в частных производных  и соблюдаются соответствующие граничные и конечные условия.

Модель Кокса-Ингерсолла-Росса (Cox-Ingersoll-Ross model)

Предполагается, что краткосрочная процентная ставка rτ в мире, нейтральном к риску, определяется стохастическим дифференциальным уравнением

Стоимость облигации с нулевым купоном номиналом 1 долл. и датой погашения Т может быть найдена по формуле, так как в данном случае:

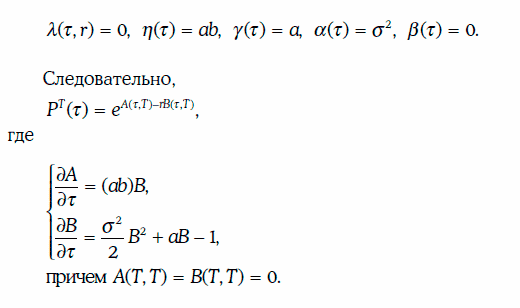
Решив систему дифференциальных уравнений, получим, что

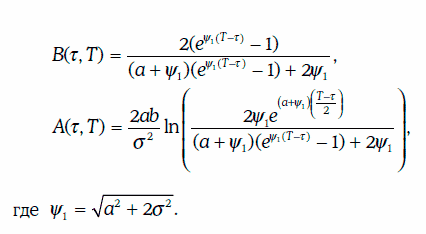
Замечание. Были выведены формулы для оценки европейских опционов на облигацию с нулевым купоном. Однако эти формулы значительно сложнее тех, которые справедливы для модели Васичека.