Точечные оценки

Среднее статистическое значение (математическое ожидание) определяется по формуле:

где n — число наблюдений (элементов выборки); Xi — результат i-го наблюдения.

Статистическая дисперсия определяется по формуле:

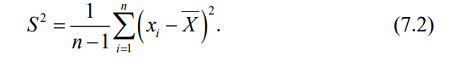
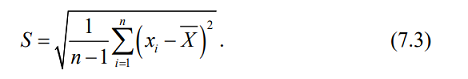
Иногда для описания случайной величины полезно знать коэффициент вариации, который вычисляется как отношение среднего квадратического отклонения к среднему арифметическому:

Необходимо найти характеристики случайной величины.

Найдем математическое ожидание с помощью формулы (7.1):

Оценку дисперсии можно найти с помощью формулы (7.2), но на практике для облегчения расчетов используют следующее соотношение:

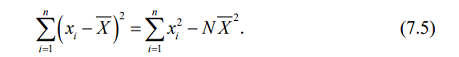
Таким образом, оценку дисперсии проще найти по формуле:

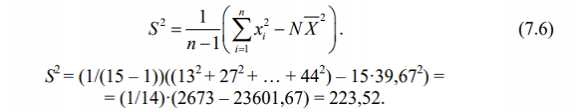
Среднее квадратическое отклонение определим как корень квадратный из дисперсии:

Коэффициент вариации определим по формуле (7.4):

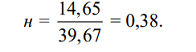
На практике, для удобства представления и обработки, данные, полученные в результате наблюдений, группируют по интервалам.

В этом случае значением, представляющим каждый интервал с количеством попаданий mj, служит середина интервала, которую вычисляют по формуле:

где хmin — наименьшее значение из данных наблюдений; Δх — величина интервала; j — номер интервала (j = 0, 1, 2, … k – 1); k — количество интервалов группирования.

Когда данные расположены по интервалам, то некоторая часть информации теряется. Так, среднее значение и дисперсия, вычисленные по сгруппированным данным, будут отличаться от значений, вычисленных по несгруппированным данным.

В случае сгруппированных данных, формулы (7.1) и (7.2) приобретают следующий вид:

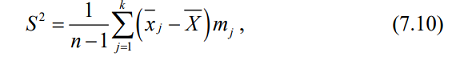
где Х j — середина j-го интервала; mj — число наблюдений в j-ом интервале.

Пример 2. Разжимные кулаки ножных тормозов автомобилей ЗиЛ-431410 заменялись в эксплуатации при превышении допустимого износа рабочих поверхностей и мест сопряжений с втулками кронштейнов. В процессе наблюдений было зафиксировано 45 первых замен разжимных кулаков. Значения наработок на отказ в тыс. км:

251,7; 201,4; 192,9; 70,0; 198,9; 133,5; 125,0; 260,6; 173,2; 223,1; 234,0; 255,3; 227,3; 144,3; 238,5; 167,6; 250,8; 217,1; 102,1; 199,2; 246,6; 163,6; 192,2; 205,2; 329,9; 283,8; 177,7; 209,6; 233,0; 165,6; 165,1; 218,3; 231,8; 145,6; 265,0; 197,6; 246,0; 139,9; 190,3; 226,5; 236,1; 223,8; 241,8; 160,0; 118,7.

Необходимо найти характеристики случайной величины.

Сгруппируем данные наблюдений.

Вычислим приближенное количество интервалов группирования по формуле Стенжерса:

Полученное значение округляем по недостатку k = 6.

Упорядочим значения наработок в порядке возрастания:

70; 102,1; 118,7; 125; 133,5; 139,9; 144,3; 145,6; 160; 163,6; 165,1; 165,6; 167,6; 173,2; 177,7; 190,3; 192,2; 192,9; 197,6; 198,9; 199,2; 201,4; 205,2; 209,6; 217,1; 218,3; 223,1; 223,8; 226,5; 227,3; 231,8; 233; 234; 236,1; 238,5; 241,8; 246; 246,6; 250,8; 251,7; 255,3; 260,6; 265; 283,8; 329,9.

Рассчитаем величину интервала группирования:

С помощью таблицы 7.1 подсчитаем число попаданий результатов наблюдений и середину каждого интервала группирования.

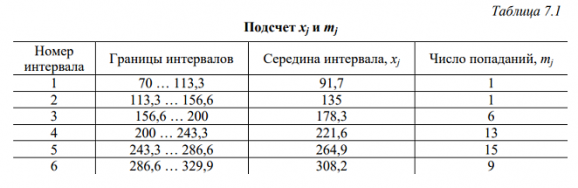
Найдем математическое ожидание с помощью формулы (7.9):

Найдем дисперсию по формуле (7.10):

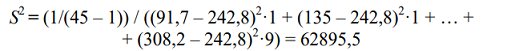
Среднее квадратическое отклонение и коэффициент вариации определяются аналогично примеру 1:

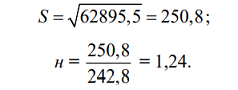
Данные числовые характеристики называют точечными, так как они характеризуют изучаемую случайную величину одним числом.

При небольшом числе испытаний указанные характеристики, как правило, отличаются от их истинных значений.