Подходы к решению транспортных задач

Существует много способов решения транспортных задач: метод потенциалов, симплекс-метод, распределительный метод и др. В зависимости от конкретной формулировки задачи и навыков исследователя применяется тот или иной метод решения.

В рамках этой главы мы с вами рассмотрим распределительный метод. Он сводится к записи первоначального решения и дальнейшему поэтапному его улучшению. Предположим, что нам нужно спланировать распределение однородного товара от трех производителей (A, B, C) к трем потребителям (D, E, F). Мощности производителей (ai) и потребности потребителей (bj) приведены в табл. 4.8.

Можно отметить, что мы имеем дело с транспортной задачей замкнутого типа, в которой суммарный объем производства (1400 тыс. ед.) равен суммарному объему потребления (1400 тыс. ед.). Стоимость доставки единицы груза от каждого производителя к каждому потребителю (cij) представлена в табл. 4.9.

В случае решения реальной задачи наиболее трудоемкой частью работы является именно определение стоимостей перевозок. Доставку груза из одного города в другой возможно осуществить с помощью различных видов транспорта и с привлечением разных транспортных компаний.

Задача логиста в этом случае состоит в тщательном расчете стоимости перевозки по каждому варианту и выборе из них минимальной. При наличии, скажем, шести распределительных центров и ста потребителей эту операцию будет необходимо проделать 600 раз.

Целевая функция этой транспортной задачи представляет собой суммарную стоимость доставки всех единиц груза от производителей потребителям. Наша задача заключается в том, чтобы найти такой набор переменных xij (объемов перевозки от i-го производителя к j-му потребителю), при котором целевая функция будет минимальна.

Первоначальное решение транспортной задачи может быть найдено несколькими способами. Наиболее распространенные – метод минимальной стоимости и метод северо-западного угла. Какой именно будет выбран метод, не имеет особенного значения. В дальнейшем это решение с большой долей вероятности потребует корректировки.

Первоначальное решение задачи, найденное по методу северо-западного угла, представлено в табл. 4.10. В углу ячейки записывается стоимость перевозки, в центре ячейки – объем перемещаемого по данному маршруту груза.

По методу северо-западного угла мы должны начать работу с левой верхней ячейки (ячейка AD). Мощность завода А составляет 200 тыс. ед., потребность города D – 600 тыс. ед. Следовательно, имеет смысл перемещать по маршруту AD максимум 200 тыс. ед. Записываем это значение в ячейку.

На этом работа со строкой А завершена: мы распределили всю продукцию, которая была доступна на данном предприятии. После исключения строки А у нас получается новая матрица размером 2 на 3 клетки. Изучим левую верхнюю ячейку этой матрицы (ячейка BD). По маршруту BD мы можем переместить максимум 400 тыс. ед. груза, так как мощность завода В составляет 600 тыс. ед., а потребитель D на данный момент недополучает 400 тыс. ед. Записываем это значение в ячейку BD.

Потребности предприятия D полностью удовлетворены; исключаем этот столбец из рассмотрения. У нас получается матрица 2 на 2 клетки (ячейки BE, BF, CE и CF). Левая верхняя из них – BE. Потребитель B желает получить 400 тыс. ед. груза, а на заводе E осталось только 200 тыс. ед. Записываем значение 200 в ячейку BE. Аналогично заполняем оставшиеся ячейки.
Рассчитаем сумму транспортных издержек для найденного первоначального решения:

F* 200 * 58* 400 *8 * 200 *4 *200 * 7 *400 * 5 * 8400 тыс. ден. ед.

Определим, насколько оптимально это решение.
Выбираем любую свободную ячейку (например, ячейку AE). Предположим, что мы хотим перевозить по этому маршруту одну единицу груза. Тогда для того, чтобы сошлась сумма по столбцу (чтобы потребитель Е получил ровно 400 тыс. ед. товара, а не больше), мы должны в этом же столбце убрать одну единицу товара. Вычитаем ее из ячейки BE.

Для того чтобы сошлась сумма по строке В, мы должны прибавить одну единицу груза в какой- либо ячейке этого столбца (например, BD). И наконец, чтобы сошлась сумма по столбцу D, мы должны вычесть одну единицу из ячейки AD. Круг замкнулся. Добавление единицы груза в первоначально выбранную нами свободную ячейку АЕ не вызывает подвижек в остальных ячейках таблицы. Покажем эти наши рассуждения наглядно (табл. 4.11).

Давайте определим, как повлияет добавление одной единицы груза на маршрут АЕ на общую сумму транспортных издержек.

AE = +4 – 4 + 8 – 5 = +3.

Следовательно, при добавлении одной единицы груза на маршрут АЕ общая сумма транспортных издержек увеличится на 3 ден. ед. Использование маршрута АЕ, таким образом, нецелесообразно.

Рассмотрим следующую свободную ячейку (CD). Если мы добавим в эту ячейку одну единицу товара, перераспределение затронет несколько ячеек: CD – BD – BE – CE. Причем в ячейках CD и BE мы прибавляем одну единицу, а в ячейках BD и CE – вычитаем. Давайте посмотрим, какое влияние окажет это перераспределение на целевую функцию.

CD = +9 – 8 + 4 – 7 = –2.

Таким образом, при добавлении единицы груза в ячейку CD целевая функция уменьшится на две денежные единицы.
Изучим остальные незанятые ячейки. Для ячейки BF маршрут пересчета затронет ячейки BF – CF – CE – BE. На сумму транспортных издержек добавление единицы груза в ячейку BF повлияет неблагоприятно.

BF = +3 – 5 + 7 – 4 = +1.

Последняя свободная ячейка (AF) для составления замкнутого цикла пересчета потребует некоторых усилий. В этом процессе будут задействованы шесть ячеек: AF – CF – CE – BE – BD – AD. Наглядно этот процесс представлен в табл. 4.12.

Определим эффект от перевозки по маршруту AF одной единицы груза:

AF = +3 – 5 + 7 – 4 + 8 – 5 = +4.

Использование маршрута AF нецелесообразно.

Таким образом, из всех имеющихся свободных ячеек имеет смысл работать только с ячейкой CD, так как только использование этого маршрута позволяет сократить общую сумму транспортных издержек. Определим, какое количество груза мы можем добавить на маршрут CD. В перераспределении принимают участие ячейки CD, BD, BE и CE (табл. 4.13). Причем в ячейки CD и BE мы прибавляем некоторое количество груза, а из ячеек CE и BD мы должны это же количество груза вычесть.

Очевидно, что чем большее значение мы добавим в ячейку CD, тем сильнее сократится общая сумма расходов на перевозку. Так как в ячейках не может находиться отрицательное значение (ограничение xij * 0 ), максимальная величина, которую мы можем добавить в ячейку CD, составляет 200 тыс. ед. Это же значение мы прибавляем в ячейку ВЕ и вычитаем из ячеек BD и CE.

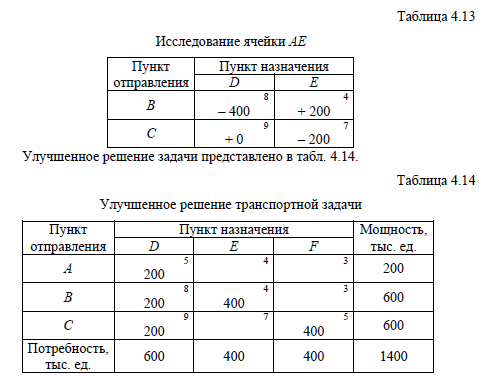
Рассчитаем суммарные транспортные издержки по этому варианту:

F * 200 * 5 * 200 * 8 * 400 * 4 * 200 * 9 * 400 * 5 * 8000 тыс. ден. ед.

Суммарные издержки сократились на 400 тыс. ден. ед. Давайте посмотрим, нельзя ли ещё немного улучшить решение. Изучаем свободные ячейки по уже знакомому алгоритму:

Интерес представляет только одна ячейка – BF. В пересчете принимают участие ячейки BF, CF, CD и BD (табл. 4.15). Максимальное количество груза, которое мы можем добавить в ячейку BF, – 200 тыс. ед.

Рассчитаем суммарные транспортные издержки по этому варианту:
F * 200 * 5 * 400 * 4 * 200 * 3 * 400 * 9 * 200* 5 * 7800 тыс. ден. ед.
Суммарные издержки сократились ещё на 200 тыс. ден. ед. Оптимально ли найденное решение? Ещё раз изучим свободные ячейки:

Как видите, при добавлении любого количества груза на любой свободный маршрут сумма транспортных издержек будет расти. Следовательно, найденное решение оптимально. Минимальная сумма транспортных издержек составляет 7800 тыс. ден. ед.