Распространение шума

Поверхность тела, совершающая колебания, является излуча­телем (источником) звуковой энергии, который создает акусти­ческое поле.

Акустическим полем называется область упругой среды, кото­рая является средством передачи акустических волн. Акустическое поле характеризуется звуковым давлением />зв (формула ( 12.1)) и акустическим сопротивлением Za (формула (12.2)). Энергетиче­скими характеристиками акустического поля являются интенсив­ность / (формула (12.3)); мощность излучения W — количество энергии, проходящей за единицу времени через охватывающую источник звука поверхность. Важную роль при расчете акустиче­ского поля играет характеристика направленности звукоизлучения — угловое пространственное распределение образующегося вокруг источника звукового давления.

Единицы измерения перечисленных величин и аналитические выражения взаимосвязи этих величин приведены в табл. 12. 1.

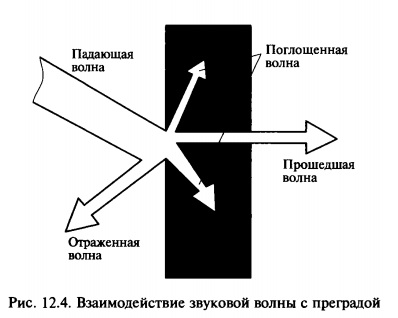
Если акустическое поле не ограничено поверхностью и рас­пространяется практически до бесконечности, то такое поле на­зывается свободным акустическим полем. В ограниченном простран­стве (например, в закрытом помещении) распространение звуко­вых волн зависит от геометрии и акустических свойств поверхно­стей, расположенных на пути распространения волн. Если звуковая волна встречает преграду с иным, чем акустическая среда, волновым сопротивлением, то часть звуковой энергии отражается от преграды, часть проникает в нее и поглощается преградой, превращаясь в тепло, а оставшаяся часть проникает сквозь пре­граду (рис. 12.4). Свойства самой преграды и материала, покрыва­ющего эту преграду, определяются следующими показателями.

1. Коэффициент звукопоглощения

где Iпогл — поглощенная материалом или преградой звуковая энер­гия; Iпат — падающая на преграду звуковая энергия.

2. Коэффициент отражения

3. Коэффициент звукоизоляции

4. Коэффициент прохождения (используются также термины «коэффициент проницаемости» и «коэффициент проникновения»)

Из определения коэффициента прохождения следует, что чем меньше значение х, тем больше ослабление звука преградой, т е. лучше ее звукоизолирующие свойства.

5. Коэффициент рассеяния от поверхности преграды

Величины коэффициентов а, р, 8, х зависят от частоты звуко­вой волны. Используя приведенные выше формулы, можно запи­сать следующие соотношения:

Звукоизоляция R, дБ, определяется по формуле

Процесс формирования звукового поля в помещении связан с явлениями реверберации и диффузии. Если в помещении начина­ет действовать источник звука, то в первый момент времени име­ем только прямой звук. По достижении волной звукоотражающей преграды картина поля меняется из-за появления отраженных волн.

Если в звуковом поле поместить предмет, размеры которого малы по сравнению с длиной звуковой волны, то практически не на­блюдается искажения звукового поля. Для эффективного отраже­ния необходимо, чтобы размеры отражающей преграды были боль­ше или равны длине звуковой волны.

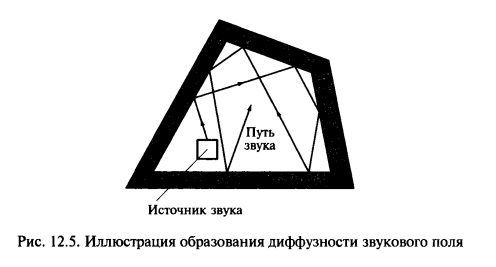
Звуковое поле, в котором возникает большое количество от­раженных волн с различными направлениями, в результате чего удельная плотность звуковой энергии одинакова по всему полю, называется диффузным полем (рис. 12.5). После прекращения ис­точником излучения звука акустическая интенсивность звукового поля уменьшается до нулевого уровня за бесконечное время.

Считается, что звук полностью затухает, когда его интенсив­ность падает в 106 раз от уровня, существующего в момент его выключения, что соответствует снижению акустического давле­ния на 60 дБ. Таким образом, любое звуковое поле как элемент колеблющейся среды обладает собственной характеристикой за­тухания звука реверберацией (послезвучание).

Шумовые характеристики оборудования оговариваются в тех­нической  документации, справочниках или могут быть получены расчетным путем.

Человек слышит звук в широком диапазоне звуковых давлений р (интенсивностей I). Стандартным порогом слышимости (или порогом слышимости) называют эффективное значение звуково­го давления (интенсивности), создаваемого гармоническим коле­банием с частотой I = 1 ООО Гц, едва слышимым человеком со
средней чувствительностью слуха. Порогу слышимости соответ­ствует звуковое давление P0 = 2 • 10^-5 Па или интенсивность звука I0 = 10~12 Вт/м2. Верхний предел звуковых давлений, ощущаемых слуховым аппаратом человека, ограничивается болевым ощуще­нием и принят равным рт= 20 Па и Im= 1 Вт/м2.

Восприятие звука человеческим ухом представляет собой слож­ный процесс. Человеческое ухо неодинаково реагирует на звуки с разными частотами. Чувствительность уха увеличивается при час­тотах от 16 до 1ООО Гц. Наибольшей чувствительностью челове­ческое ухо обладает в диапазоне частот от 1ООО до 4000 Гц, где она практически постоянна. После частоты 4000 Гц чувствитель­ность уха снова уменьшается. Анализ кривых равной громкости (рис. 12.6), построенных на основе экспериментальных исследо­ваний Флетчера и Мунсона показывает, что для того чтобы услы­шать низкий тон с частотой 50 Гц, требуется звуковое давление,
в 100 раз превышающее звуковое давление, соответствующее тону с частотой 1000 Гц.

 

Человек воспринимает звуковое давление и оценивает гром­кость этого сигнала. Уровень громкости звука измеряется физи­ческой величиной — фоном. Уровень одинаковой громкости зву­ковых сигналов в фонах на разных частотах не cоответствует уровню звукового давления в децибелах; они совпадают лишь на час­
тоте 1 ООО Гц.

Для анализа акустических характеристик различных объектов пользуются единицей измерения — децибел (дБ), названной в честь Грейма—Бела. Увеличение интенсивности звука в 10 раз соответ­ствует белу (Б): 1Б = 10 дБ.

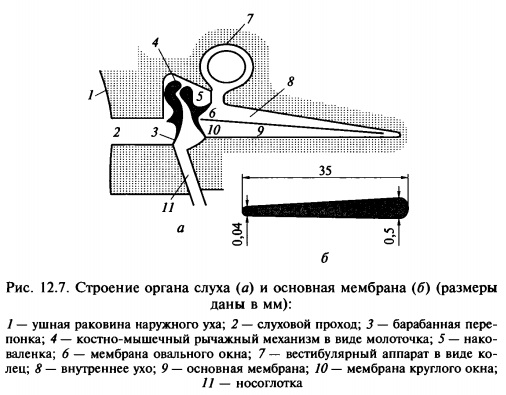
Необходимость введения поправок обусловлена несоответствием уровней громкости (см. рис. 12.6), воспринимаемых человеческим ухом (рис. 12.7), уровням звуковых давлений на частотах, отлич­ных от восприятия на стандартной частоте 1ООО Гц.

Для оценки и сравнения звукового давления р, Па, интенсив­ности I, ВТ/м2, и звуковой мощности W, Вт, различных исто­чников, учитывающих психофизическое восприятие звука челове­ком, приняты характеристики их уровней L (с cоответствующим индексом), выраженные в безразмерных единицах — децибелах, дБ:

где W0 — опорная звуковая мощность на частоте 1000 Гц, W0 – = 10^- 12 Вт.

Предположим источник излучает на определенной частоте зву­ковую мощность 1О^-6 Вт. Тогда уровень звуковой мощности Lw со­ставит 60 дБ.

Безразмерные величины Lp, Lh Lw достаточно просто измеря­ются приборами, поэтому их полезно использовать для определе­ния абсолютных значений р, I, W по обратным к формулам (12.5) зависимостям:

Пусть источник звука окружен некоторой замкнутой поверх­ностью S так, что направление распространения волн в любой точке поверхности перпендикулярно этой поверхности.

Если вся площадь поверхности разделена на n равных частей dS с давлением на каждой площадке рi а число п велико, то уравнение для W приобретает вид

где р*ср — среднеквадратическое значение звукового давления по всей площади поверхности,

Подставим значение W из формулы (12.7) в формулу (12.5) и получим значение уровня звуковой мощности, выраженное через параметры среды и звуковое давление:

Используя выражение (12.6) для определения рi^2 = рo^2 10^(0,1Lpi), выразим значение Pcp^2 через уровни звукового давления Lpi на эле­ментарной площадке:

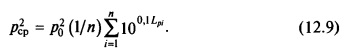
Подставим формулу (12.9) в (12.8) и получим уровень звуко­вой мощности

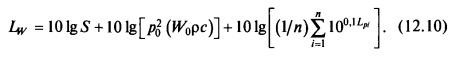
Второй член уравнения (12.10) при значениях р0 = 2 *10^-5 Па, W0 = 10^-12 Вт, рс = 415 кг/(м^2- с) равен 0,2 и его значением можно пренебречь по сравнению с реальными значениями других членов.

Таким образом, имеем

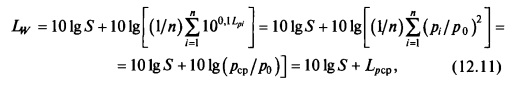
где Lpcp — средний уровень звукового давления, или уровень сред­неквадратического значения звукового давления.

Средний уровень звукового давления определяют по формуле

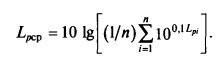
Уравнение (12.11) описывает приближенное соотношение меж­ду уровнем звуковой мощности и средним уровнем звукового дав­ления, что позволяет определить уровень звуковой мощности, измеряя уровень звукового давления на воображаемой поверхно­сти, окружающей источник. Уравнение (12.11) справедливо приопределении звукового давления в свободном звуковом поле, в остальных случаях его можно использовать, принимая соответ­ствующие поправки.

Предположим, что имеются два чистых тона с частотами f1 и f2 в звуковом поле, среднеквадратические значения звукового дав­ления которых равны соответственно р1 и р2. Суммарное средне­квадратическое значение звукового давления р в этом случае по­лучим суммированием двух синусоидальных волн:

Подставим формулу (12.12) в (12.5) и получим

или с учетом формулы ( 12.6 ):

Например, если два чистых тона имеют одно и то же средне­квадратическое значение звукового давления р { = р2, а значит, один и тот же уровень звукового давления ЬрХ = Ьр2, то создава­емый ими суммарный уровень звукового давления в соответствии
с уравнением (12.13) будет равен

т.е. на 3 дБ больше, чем уровень звукового давления одного от­дельно взятого тона. В общем виде для л-го количества чистых то­нов с разными частотам будем иметь:

Отметим, что суммарный уровень звукового давления от не­скольких звуковых волн различных частот не зависит от соотно­шения фаз звукового давления в этих волнах. Однако сочетание двух звуковых волн одной и той же частоты зависит от соотноше­ния фаз. Такие колебания называются когерентными.

Рассмотрим случай двух звуковых волн одной и той же частоты в звуковом поле. Среднеквадратическое значение звукового давле­ния в данной точке поля двух сигналов одной частоты с разно­стью фаз 0 определяется из уравнения суммирования векторов:

где р\ и р 2 — среднеквадратические значения звуковых давлений двух звуковых волн; 0 — фазовый угол между двумя звуковыми волнами в данной точке.

Если р\=р2 и две звуковые волны в какой-либо точке находят­ся в противофазе, т.е. 0 = 180 °, то результирующее звуковое давле­ние в этой точке равно нулю. С другой стороны, если две звуковые волны находятся в фазе друг с другом, т.е.

то уровень звукового давления Lp = 10 lg(4p1/p0)^2 = 10 lg(p1/po)^2 + 10 lg(4) =Lpi + 6 возрастает на 6 дБ.